コンピュータセキュリティとフォレンジックにおけるハッシュ関数と公開鍵暗号

ハッシュ関数の紹介：#

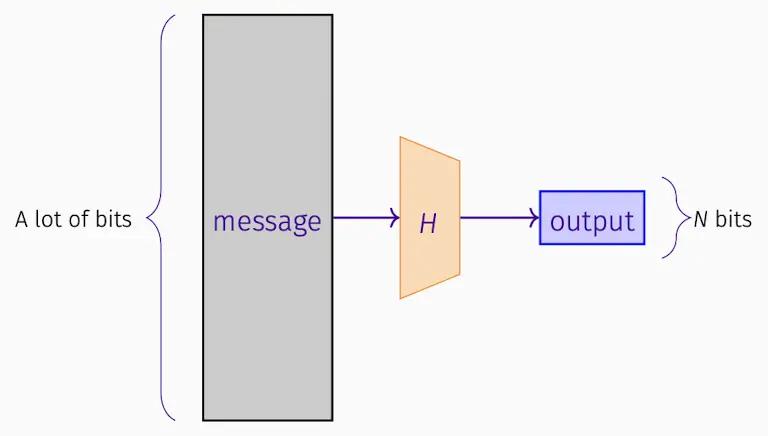
Screenshot_2024-03-14_at_20.37.50 !

ハッシュ関数は、任意の長さの入力文字列を固定長のハッシュ値（時にはメッセージダイジェストと呼ばれる）にマッピングする効率的に計算可能な関数です。入力が何ビットであっても、出力は N ビットです。
ハッシュ関数は、keyed primitive に基づく原語ではありません。

ハッシュ関数の応用#

メッセージフィンガープリンティング、ファイル整合性チェック、署名スキーム（ハッシュ後署名のパラダイム）、メッセージ認証コード（例：HMAC）、鍵派生（例：Diffie-Hellman 鍵交換における「原データ」からの鍵派生）、パスワードハッシュ、コミットメントスキーム、擬似乱数生成器、ストリーム暗号（カウンターモードでのハッシュ関数）、ビットコイン（プルーフ・オブ・ワークスキーム）、ポスト量子署名スキームなど。

ハッシュ関数の標準：#

NIST の SHA-1（2010 年まで）、SHA-2（SHA-224、SHA-256、SHA-384、SHA-512）、SHA-3（Keccak）；NESSIE の SHA-2（SHA-256、SHA-384、SHA-512）、WHIRLPOOL；CRYPTREC の SHA-2（SHA-256、SHA-384、SHA-512）。

パスワードハッシュ#

暗号化ハッシュ関数はさまざまなセキュリティ環境で使用できますが、最も有名なのはパスワードハッシュです。

サーバー内のパスワードはプレーンテキストであり、サーバーが侵害されると直接漏洩し、攻撃者が成りすますことができます。
データベースにはパスワードハッシュ値のみを保存します。
各ユーザーの H (password) を保存し、パスワードを保存しません。
サーバーは受け取ったパスワードをハッシュし、テーブルと比較します。一致すれば認証成功です。
直感的には、攻撃者はパスワードを復元するために逆ハッシュを行う必要があります。

ソルト#

各ハッシュ計算にランダムでアカウント専用の値を追加します。これをソルトと呼びます。
典型的なソルト値は 64 ビットで、衝突を防ぐのに十分です。

サーバーは (salt, H (salt||password) を保存し、H (Password) ではなく、salt は特定のアカウントのランダム値です。

イテレーション#

典型的なイテレーション回数は 10000 で、各パスワードを試すたびに 10000 回計算し、安全性が向上します。

ハッシュ関数の安全属性#

定理#

衝突：ハッシュ後の値が等しいが、ハッシュ前の値は等しくない。

抗衝突性は、第二前画像抵抗性に対するものであり、任意の衝突抵抗性を持つハッシュ関数は第二前画像抵抗性を持ちます。

前画像抵抗と衝突抵抗#

前画像抵抗（単方向性）：h があるとき、m を見つけることができない。
第二前画像抵抗：m1 が与えられたとき、別の m2 のハッシュが m1 のハッシュと等しい場合、m2 は m1 と等しくない。
衝突抵抗：m のペアにおいて、H (m1)=H (m2) であれば、m1 は m2 と等しくない。
ニア・コリジョン抵抗：ハッシュ値がほぼ同じ m1 と m2 も異なる、信号中の公開鍵検証に現れます。
部分前画像抵抗 1：与えられたハッシュ値から情報を復元できない。
部分前画像抵抗 2：長さ l のハッシュ値が与えられたとき、2l 回の試行内でそのメッセージを取得できない。

t 時間内に実行されるすべての A に対して、A が衝突を出力する確率の境界は e です。

バースデー制約の意味#

N ビットのハッシュ関数は、一般的な衝突攻撃に対抗するために N/2 ビットの安全性しか提供できません。例えば、128 ビットの安全性を実現するためには 256 ビットの出力のハッシュ関数が必要です。
しかし、現在のところ、一般的なバースデー攻撃（2^128）よりも速い衝突発見攻撃はありません。
一部のコストモデルでは、攻撃コストは 2^(N/2) の「操作」+ メモリです。

通常のハッシュ関数は暗号には適していません！非暗号ハッシュ関数は（暗号において）非常に弱いです！#

メルクル・ダムガード反復ハッシュ#

圧縮関数 h を使用してハッシュ関数を構築します。
メッセージを固定長 k のブロック（例：m1、m2）に分割し、パディングを含めます。
IV を導入して m1をハッシュし、その後m2を導入して手順を繰り返します。
圧縮関数 h が抗衝突性を持つ場合、H も抗衝突性を持ちます。

長さ拡張特性#

本来は tu で出力されるべきですが、次のブロックへの入力として使用されます。

MAC や鍵導出のような特定のアプリケーションで問題が存在します。ハッシュ値関数から構築された関数に鍵と情報を接続します。

主な問題は、ハッシュ出力サイズ = ブロック暗号ブロックサイズであるため、2N/2 のバースデー攻撃を回避するために大きなブロックサイズ N が必要です。

ブロック暗号から圧縮関数を構築#

デイビス・マイヤー：#

連鎖変数が情報入力に変わり、情報入力が鍵になります。

抗衝突性を提供します。

SHA-2#

デイビス・マイヤーモードの 256 ビットブロック暗号を使用して圧縮機能を構築しました。

速度は SHA-1 の 2 倍です。

SHA-3#

可変長出力を許可し、鍵導出などのアプリケーションで非常に便利です。

SHA3-256 は SHA-256 よりもわずかに遅い（10-15%）。

公開鍵暗号（PKE）#

公開鍵暗号技術の基礎は非対称暗号メカニズムであり、従来の対称暗号とは異なり、非対称暗号は一対の鍵：公開鍵と秘密鍵を使用します。公開鍵は情報を暗号化するために使用され、秘密鍵は情報を復号化するために使用されます。この 2 つの鍵は数学的に関連していますが、公開鍵から秘密鍵を簡単に計算することはできず、これにより情報伝送の安全性が確保されます。

三重アルゴリズム：#

KGen: ランダムな鍵ペア (sk, pk) を生成します。sk は秘密鍵、pk は公開鍵です。
Enc: 一般的にはランダムで、pk + m → c
Dec: sk + c → m

![Screenshot_2024-03-15_at_03.28.22](https://file.yotroy.cool/Screenshot_2024-03-15_at_03.28.22.png?x-oss-process=style/1)

プロセス#

実際のアプリケーションでは、教科書の RSA のように直接使用すべきではありません。

Screenshot_2024-03-15_at_03.35.19

Screenshot_2024-03-15_at_03.45.11

Screenshot_2024-03-15_at_03.48.42

破解の重要点#

秘密鍵を推測しにくく保護するだけでなく、情報の機密性を確保する必要があります。より正確には、選択暗号文攻撃（IND-CCA）下での不可区別性です。
敵が任意のメッセージの復号化を取得できた場合でも、平文に関する情報が敵に漏れるべきではありません。
敵は暗号化と復号化のオラクルにアクセスでき、鍵ペア (sk, pk) にそれぞれ使用します。
敵は任意のメッセージペア (m0, m1) を暗号化オラクルに提出し、暗号化メッセージ c を受け取ります。
敵はまた、任意の暗号文 c' を復号化オラクルに提出し、復号化メッセージ Dec_sk (c') を受け取ります。
敵の目標はビット b を復元することです。
この定義は IND-CPA の定義と比較されますが、敵はここで暗号化オラクルの出力を提出できません。そうでなければ、彼らは簡単に試合に勝つことができます。

IND-CCA 選択暗号文攻撃下の不可区別性#

選択暗号文攻撃（CCA）下の不可区別性（IND）

Screenshot_2024-03-15_at_03.55.17

攻撃者が何らかの方法で公開鍵 (pk) から秘密鍵 (sk) を復元できる場合、その PKE スキームは IND-CCA 安全ではありません。
あるスキームが IND-CCA 安全であるならば、それは必然的に IND-CPA 安全です。
もし PKE スキームに決定論的暗号化アルゴリズムがあるならば、それは IND-CPA 安全ではありません。
教科書の RSA は決定論的であるため、IND-CPA 安全でも IND-CCA 安全でもありません。実際のアプリケーションでは、RSA は OAEP のようなパディングスキームを使用してランダム性を追加し、IND-CPA および IND-CCA 安全性を達成する必要があります。

使用例#

RSA 因数分解、ElGamal 離散対数、McEliece コードベースの暗号法、NTRUEncrypt 格子ベースの暗号法

得意なこと？#

PIN コード（支払い用など）
対称暗号よりも高価
PKE は通常、対称鍵を伝送するために使用され、バルクまたはペイロードデータを暗号化します。
PKE のこの使用法は通常、混合暗号と呼ばれます。
対称鍵は対称暗号スキームで実際のデータを暗号化するために使用されます。

鍵封装メカニズム KEM#

選択暗号文攻撃（CCA）下の不可区別性（IND）、つまり IND-CCA 安全性を反映しています。

Screenshot_2024-03-15_at_04.05.22

混合暗号#

一般に KEM/DEM パラダイムと呼ばれます。
開発プロセスを簡素化し、開発者がペア暗号原語を必要としないため、複雑さとエラーの可能性を減少させます。
KEM（鍵封装メカニズム）を利用して対称鍵を安全に伝送し、DEM（データ封装メカニズム）を使用して対称鍵でデータを暗号化します。

定理#

PKE システムは鍵封装メカニズム（KEM）とデータ封装メカニズム（DEM）から構築されており、KEM が選択暗号文攻撃（IND-CCA）安全であり、DEM も IND-CCA 安全であれば、全体の PKE システムも IND-CCA 安全です。

対称暗号スキームの核心的な問題は、暗号鍵を事前に共有する必要があることです。この問題を解決するために、公開鍵暗号メカニズムがあります。PKE を鍵封装メカニズムとして形式化し、混合暗号を構築し、KEM/DEM パラダイムを使用してその安全性を証明する方法を示します。要約は以下の通りです：

対称暗号（SE）は鍵を事前に共有する必要があり、分散環境では不便です。これが公開鍵暗号（PKE）が必要な理由であり、鍵配布の問題を解決します。
しかし、PKE は対称暗号に比べて計算コストが高いです。効率を保つために、PKE で短い鍵を暗号化し、その鍵を使用して対称暗号（SE）でペイロードデータを暗号化します。この方法は通常、混合暗号と呼ばれます。
PKE の使用を鍵封装メカニズム（KEM）として形式化し、KEM/DEM パラダイムを通じて混合暗号を構築し、その安全性を証明する方法を示します。

要するに、混合暗号は PKE の安全性と SE の効率を組み合わせ、鍵封装とデータ封装の 2 つのステップを通じて、安全かつ効率的に暗号鍵とデータを伝送します。