XOR#
XOR is short for "exclusive or," a fundamental bitwise operation. Its rule is to compare two bits; if the two bits are the same, the result is 0; if the two bits are different, the result is 1.


Since ≠ 0.5, there is information. Thus, even with just one subset of values, the deviation can be exploited in a roughly similar manner. Even 0.5000001.
source of info = If the degree of consistency between the input expression and the output expression does not exceed 0.5, then one expression is the source of information for the other expression.

Linear Cryptanalysis#
- Plaintext and ciphertext are visible
- It is a known plaintext attack
- A sufficient number of plaintext and ciphertext pairs are needed to find the linear relationship between input bits and output bits.
- Requires sufficiently good linear approximations.
- Refers to a type of attack aimed at block ciphers.
- Approximates block ciphers using linear expressions (some variables represented by mod-2 bit operations).
- The truth (or falsehood) of these expressions carries a certain deviation, which is used to discover key bits.
Substitution Boxes (S-box)#
- Determine the bias of the S-box and construct the LAT.
- Use (biased) linear expressions.
- Link expressions from the initial plaintext to the intermediate ciphertext.
- Through Matsui's bias theorem.
- For the final subkey, determine the frequency of the expression's validity.
- If the bias matches, you have discovered the key!
- Repeat the above steps for each subkey.

Implemented in the form of a lookup table, but cannot scale with increasing input size, so outputs must be computed differently, i.e., calculated as expressions of input bits. e.g.

Approximating Sboxes#
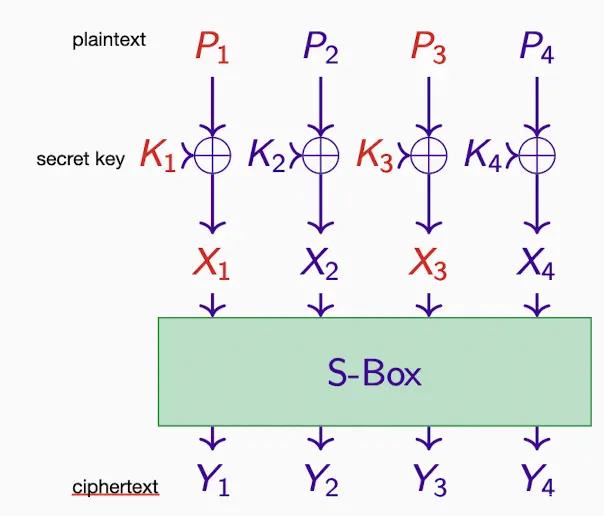
one key XORing and one Substitution Box
Assuming X3 ⊕ X4 = Y1 ⊕ Y4,
then K3 ⊕ K4 = P3 ⊕ P4 ⊕ Y1 ⊕ Y4

Linear Approximation Table (LAT) for S-boxes#

Analysis:
- x represents input, y represents output
- This is the bias table:
- 0 means unbiased, so probability is 0.5.
-
- means the actual occurrence is more than expected, - means the actual occurrence is less than expected
- Non-zero indicates information; the larger the absolute value, the more information it contains

A[1,2] means the input mask is '01', which means we only care about the second bit of the input. The output mask is '10', which means we only care about the first bit of the output.
Calculate the XOR value of the output bit corresponding to each input#
We need to perform the following sub-steps for each input:
- Look at the output value of that input in the S-box.
- Apply the input mask to the input value, keeping only the bits where the mask corresponds to 1.
- Apply the output mask to the output value, similarly keeping only the bits where the mask corresponds to 1.
- Calculate the XOR value of these two bits.
01 00 11 10 → 1010
11 01 10 00 → 1010
XOR → 0000 = 4/4
so answer is +2
also for B answer is -2
Matsui’s Piling Up Lemma#
Used to calculate the bias of multiple variables
- e.g.: bias is not 0

- e.g.: As long as one is 0, the final result is unbiased. Example Z2 is unbiased, effectively randomizing Z1 ⊕ Z2

- Conclusion: The formula is as follows

Linking S-box Approximations#
Steps:
- How to calculate probability? Based on input rather than output, as illustrated to derive the approximation of G2
- With the approximation, subtract the expected probability (usually 1/2) to get the bias
- Common XOR, eliminate intermediate nodes to move to the right side of the equation, turning it into a probability of =0
- Substitute into Matsui’s Lemma formula to find that value

- Continue calculating the overall, as illustrated
- In the substitution steps, G2 appears, so XOR becomes 0, moving to the right side of the equation
- At the same time, the probability of =1 is calculated as 5/8

- Transformation example

- Calculation example

- The transformation of the above XOR formula, so the result is the same

- Summary of the above transformations

Discovering Keys#
Visible?#
- The system only has plaintext P and ciphertext C visible, after all, it is linear cryptanalysis

Final Round Key#
The last round S-box is invertible, so the corresponding U can be calculated.
For any round key guessed by the cryptanalyst, they can generate U.

- Assume a last round key, obtaining the intermediate ciphertext, which represents the intermediate steps U1, U2, U3, U4, etc., in the encryption process.
- If the guessed key is correct, then the intermediate ciphertext is correct.
- Next, with P and U and C, calculate the approximate expression (approx. expression), which has a certain bias (bias), such as 1/8 or 3/8.
- If this approximate expression matches the observed bias, then the assumed key can be considered correct.
- If the guessed key is incorrect, then the intermediate ciphertext is also incorrect.
- If one or more key bits are guessed incorrectly, then this approximate expression will only hold true half the time, as the result is randomized.
Therefore, by comparing the approximate expression under the assumed key with the bias of 1/2, one can distinguish between correct and incorrect key guesses. Finally, try all possible last round keys to see which (P,U) approximation is least consistent with the bias of 1/2; this key is likely the actual key.
Applying#
Substitution Permutation Network (Hey’s Cipher)#
- In this system, Heys' Cipher enhances the security of encryption through repeated substitution and permutation operations and key mixing.
- 3 rounds S-box: XORing, all S-boxes are the same.
- P-box: Permutation box, permuting, it rearranges bits according to specific rules to diffuse any changes in input during each round.
- 16-bit subkeys: Assumed to be independently generated, usually obtained through key scheduling, similar to the approach in DES (Data Encryption Standard).
- Example: Each probability is based on input.
- Key mixing uses bitwise XOR operations.

-
E2E refers to end-to-end approximation, the entire encryption process from plaintext to ciphertext.


If you have enough plaintext-ciphertext pairs, theoretically, you can use this linear approximation to decrypt or more accurately guess the key.
-
How to calculate? Similarly, Matsui’s Lemma


Key sub-blocks and reverse engineering:
- Goal: Generate Intermediate Ciphertexts through K5 and C (the second and fourth subsets)
- Unrelated to the 1st and 3rd subsets, so the interest is in the 2nd and 4th.
From C to U, the correct K yields the correct U, and vice versa.


Try All Subkeys#
- The table only shows a portion of the subkeys, assuming there are 64 subkeys.
- Assuming there are 10,000 plaintext-ciphertext pairs, using 64 subkeys.
- For each p-c pair, c and subkey generate p, calculating the bias.
- The subkey with the largest bias is usually correct, but not always.
- It can be seen that when the subkeys are 24, the bias is the largest, a candidate.
