𝖄𝕺🌎𝕿𝕽𝕺¥

XOR#

XOR は「排他的論理和」の略で、基本的なビット演算の一つです。その演算ルールは、2 つのビットを比較し、同じであれば結果は 0、異なれば結果は 1 です。

なぜ≠ 0.5 なのか、それは情報があるからです。したがって、たとえ 1 つのサブセットの値しかなくても、偏差を利用して大体同じように活用できます。たとえ 0.5000001 であっても。

情報源 = 入力式と出力式の一致度が 0.5 を超えない場合、1 つの式はもう 1 つの式の情報源です。

線形暗号解析#

• 平文と暗号文が見える
• これは既知平文攻撃です
• 入力ビットと出力ビットの間の線形関係を見つけるために十分な数の平文と暗号文の対が必要です。
• 十分に良い線形近似が必要です。
• ブロック暗号に対する攻撃の一種です。
• 線形式（mod-2 ビット演算で表されるいくつかの変数）を用いてブロック暗号に近似します。
• これらの式の真（または偽）には一定の偏差があり、その偏差を利用して重要なビットを発見します。

置換ボックス (S-box)#

1. S ボックスの偏差を特定し、LAT を構築します。
2. （偏差のある）線形式を使用します。
3. 初期平文から中間暗号文へのリンク式。
4. 松井の偏差定理を通じて。
5. 最後のサブキーについて、式の成立頻度を特定します。
6. 偏差が一致すれば、キーを発見したことになります！
7. 各サブキーについて上記のステップを繰り返します。

テーブル形式で実装されますが、入力量が増えるにつれて拡張できないため、出力を異なる方法で計算する必要があります。つまり、入力ビットの式を使って計算します。例：

S ボックスの近似#

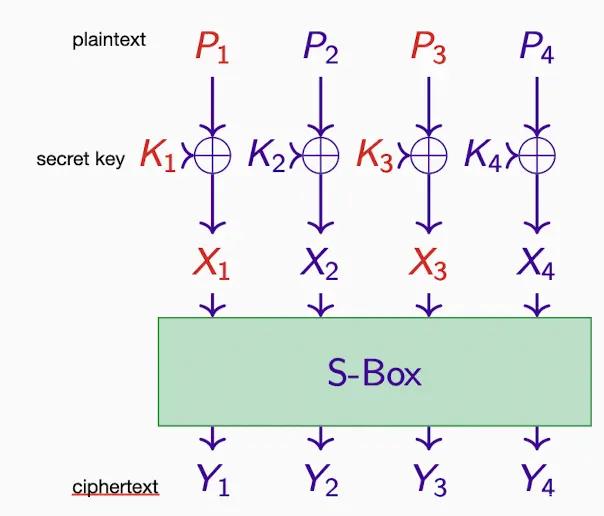
1 つのキーの XOR と 1 つの置換ボックス

仮定：X3 ⊕ X4 = Y1 ⊕ Y4、

したがって K3 ⊕ K4 = P3 ⊕ P4 ⊕ Y1 ⊕ Y4

S ボックスの線形近似テーブル (LAT)#

分析：

• x は入力を表し、y は出力を表します。
• これは偏差表です：
  • 0 は無偏を示し、probability は 0.5 です。
  • + は実際に予想より多く出現したことを示し、- は実際に予想より少なかったことを示します。
• 0 でない場合は情報があることを示し、絶対値が大きいほど情報が多く含まれます。

A [1,2] は入力マスクが '01' であることを意味し、これは入力の第 2 ビットのみを気にすることを意味します。出力マスクは '10' で、これは出力の第 1 ビットのみを気にすることを意味します。

各入力に対応する出力ビットの XOR 値を計算する#

各入力に対して以下のサブステップを実行する必要があります：

1. S ボックスでその入力の出力値を確認します。
2. 入力マスクを入力値に適用し、マスクに対応するビットが 1 のビットのみを保持します。
3. 出力マスクを出力値に適用し、同様にマスクに対応するビットが 1 のビットのみを保持します。
4. これら 2 つのビットの XOR 値を計算します。

01 00 11 10 → 1010

11 01 10 00 → 1010

XOR → 0000 = 4/4

したがって、答えは + 2 です。

B の場合も答えは - 2 です。

松井の積み上げ補題#

複数の変数の偏差を計算するために使用されます。

• 例：偏差が 0 でない

• 例：1 つでも 0 があれば、最終結果は無偏になります。例 Z2 は無偏で、Z1 ⊕ Z2 を効果的にランダム化しました。

• 結論：公式は以下の通りです。

S ボックス近似のリンク#

ステップ：

• 確率をどのように計算しますか？入力に基づいて、出力ではなく、図の例から G2 の近似値を導き出します。
• 近似値が得られたら、期待確率（通常は 1/2）を引いて偏差を得ます。
• 共通の XOR を取り、中間ノードを消去して等号の右側に移動し、=0 の確率を求めます。
• 松井の補題の公式に代入してその値を求めます。

• 全体を計算し続けます。以下の例を参照してください。
  • 置換ステップで G2 が出現するため、XOR は 0 になり、等号の右側に移動します。
  • 同時に = 1 の確率を 5/8 として求めます。

• 変換例

• 計算例

• 上記の XOR 公式の変換により、結果は同じです。

• 上記の変換のまとめ

鍵の発見#

可視化？#

• このシステムでは、平文 P と暗号文 C のみが可視化されます。結局のところ、線形暗号解析です。

最終ラウンドキー#

最後のラウンドの S ボックスは可逆的であるため、対応する U を計算できます。

暗号解析者が推測した任意のラウンドキーに対して、彼らは U を生成できます。

1. 最後のラウンドキーを仮定し、中間暗号文を得ます。これは暗号化プロセスの U1、U2、U3、U4 などの中間ステップを表します。
2. 推測したキーが正しければ、中間暗号文も正しいです。
3. 次に、P と U と C を使って近似式（approx. expression）を計算します。これは一定の偏差（bias）を持ち、例えば 1/8 または 3/8 です。
4. この近似式が観測された偏差と一致すれば、仮定したキーが正しいと見なされます。
5. 推測したキーが間違っている場合、中間暗号文も間違っています。
6. 1 つまたは複数のキーのビットが間違っている場合、この近似式はランダム化されるため、成立するのは 1/2 の確率になります。

したがって、仮定したキーの近似式と 1/2 の偏差を比較することで、正しいまたは間違ったキーの推測を区別できます。最後に、すべての可能な最後のラウンドキーを試して、(P,U) の近似値が 1/2 の偏差と最も一致しないものを見つけると、そのキーが実際のキーである可能性が高いです。

適用#

置換置換ネットワーク（Hey's Cipher）#

• このシステムでは、Heys' Cipher が繰り返しの置換と置換操作、及びキー混合を通じて暗号化の安全性を強化します。
• 3 ラウンド S ボックス：XORing、すべての S ボックスは同じです。
• P ボックス：置換ボックスで、特定のルールに従ってビットを再配置し、各ラウンドの入力の変更を拡散します。
• 16 ビットサブキー：独立して生成されると仮定され、通常はキー計画を通じて得られ、DES（データ暗号化標準）での方法に似ています。
• 例：各確率は入力です。
• キー混合はビットごとの XOR 操作を使用します。

• E2E は、平文から暗号文への全体の暗号化プロセスを指します。

  

  

  十分な数の平文 - 暗号文の対があれば、理論的にはこの線形近似を利用して復号化したり、より正確にキーを推測したりできます。

• どのように計算しますか？ 同様に松井の補題を使用します。

  

  

  重要なサブブロックと逆推：

  • 目標：K5 と C（第 2 および第 4 のサブセット）を通じて中間暗号文を生成します。
  • 第 1 および第 3 のサブセットとは無関係であるため、関心は第 2 および第 4 です。

  C から U へ、正しい K が正しい U を得ます。その逆もまた然りです。

  

  

  すべてのサブキーを試す#

  • 表には一部のサブキーのみが表示されており、64 個のサブキーがあると仮定します。
  • 10000 個の平文 - 暗号文の対があり、64 個のサブキーを使用します。
  • 各 p-c 対について、c とサブキーから p を生成し、偏差を計算します。
  • 偏差が最も大きいサブキーが通常は正しいですが、必ずしもそうではありません。
  • サブキーが 24 のときに偏差が最大で、候補となります。