𝖄𝕺🌎𝕿𝕽𝕺¥

XOR#

XOR 是 “異或” 運算的簡稱，是一種基本的位運算。它的運算規則是對兩個比特位進行比較，如果兩個比特位相同，則結果是 0；如果兩個比特位不同，則結果是 1。

因為≠ 0.5，所以是有信息的。那么即使只有一個子集的值，也能以大致相同的方式利用偏差。甚至 0.5000001。

source of info = 如果輸入表達式與輸出表達式的一致程度不超過 0.5，那麼其中一個表達式就是另一個表達式的信息源。

Linear Cryptanalysis#

• 明文和密文可見
• 是 known plaintext attack
• 足夠多的明文和密文對來尋找輸入位和輸出位之間的線性關係。
• 要求足夠好的線性逼近。
• 指針對塊密碼發起的一類攻擊。
• 通過線性表達式（用 mod-2 比特運算表示的一些變量）來逼近塊密碼。
• 這些表達式的真（或假）帶有一定的偏差，利用這種偏差來發現關鍵比特。

Substitution Boxes (S-box)#

1. 確定 S 框的偏差、構建 LAT。
2. 用 (有偏差的）線性表達式。
3. 鏈接表達式從初始明文到中間密文。
4. 通過 Matsui 的偏差定理。
5. 對於最後的子鍵，確定表達式的成立頻率
6. 如果匹配偏差，你就發現了密鑰！
7. 對每個子鍵重複上述步驟。

以查找表的形式實現的，但不能隨著輸入量的增加而擴展，因此必須以不同的方式計算輸出，即以輸入位的表達式來計算。e.g.

Approximating Sboxes#

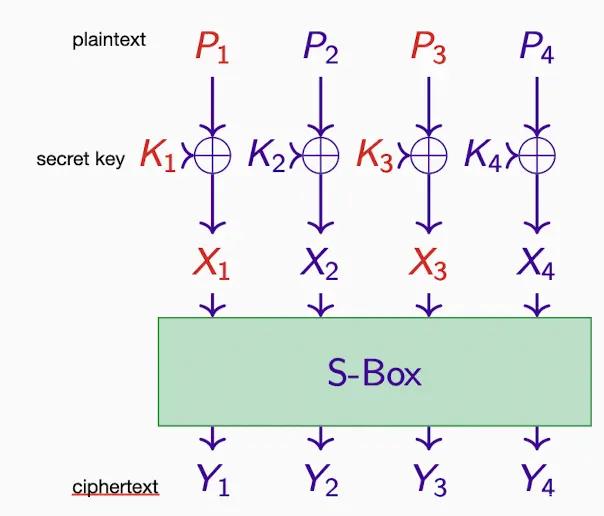
one key XORing and one Substitution Box

假設 X3 ⊕ X4 = Y1 ⊕ Y4，

那麼 K3 ⊕ K4 = P3 ⊕ P4 ⊕ Y1 ⊕ Y4

Linear Approximation Table (LAT) for S-boxes#

分析：

• x 表示輸入，y 表示輸出
• 這是偏差表：
  • 0 表示無偏，則 probability 為 0.5。
  • + 表示實際出現比預期多了，- 表示實際出現比預期少了
• 不為 0 則表示有信息，絕對值越大包含信息越多

A [1,2] 意味著輸入掩碼為 '01'，這意味著我們只關心輸入的第二位。輸出掩碼為 '10'，這意味著我們只關心輸出的第一位。

計算每個輸入對應的輸出位的 XOR 值#

我們需要對每個輸入執行以下子步驟：

1. 查看 S-box 中該輸入的輸出值。
2. 將輸入掩碼應用於輸入值，只保留掩碼對應位為 1 的位。
3. 將輸出掩碼應用於輸出值，同樣只保留掩碼對應位為 1 的位。
4. 計算這兩個位的 XOR 值。

01 00 11 10 → 1010

11 01 10 00 → 1010

XOR → 0000 = 4/4

so answer is +2

also for B answer is -2

Matsui’s Piling Up Lemma#

用來計算多個變量的偏差

• e.g. ：bias 不為 0

• e.g.： 只要有一個為 0，最終結果就是無偏。例子 Z2 是無偏的，有效地隨機化了 Z1 ⊕ Z2

• 結論：公式如下

Linking S-box Approximations#

步驟：

• 如何計算 probability？根據input而不是 output，如圖例子得出 G2 的近似值
• 有了近似值，減去預期概率（一般是 1/2）得到 bias
• 共同 XOR，消掉中間節點變到等號右邊，變成求 = 0 的概率
• 帶入 Matsui’s Lemma 公式求該值

• 繼續算整體的，例子如下
  • Substituting 步驟中都出現了 G2，所以 XOR 變成 0，變到等號右邊
  • 同時求出 = 1 的概率為 5/8

• 轉換例子

• 計算例子

• 上例 XOR 公式的轉換，所以結果一樣

• 以上轉換的總結

Discovering Keys#

可見？#

• 該系統只有 plaintext P 和 ciphertext C 可見，畢竟是線性密碼分析

Final Round Key#

最後一輪 S-box 是可逆的 invertible，所以可以算出對應的 U

對於密碼分析者猜測的任何一輪密鑰，他們都能生成 U

1. 假設一個最後一輪密鑰，得到中間密文，這代表了加密過程中的 U1, U2, U3, U4 等中間步驟。
2. 如果猜測的密鑰是正確的，那麼中間密文就是正確的。
3. 接下來，有了 P 和 U 和 C 計算近似表達式（approx. expression），它有一定的偏差（bias），比如 1/8 或者 3/8。
4. 如果這個近似表達式與觀察到的偏差匹配，那麼可以認為假設的密鑰是正確的。
5. 如果猜測的密鑰是錯誤的，則中間密文也是錯誤的。
6. 如果一個或多個密鑰位猜錯了，那麼這個近似表達式將只會有 1/2 的時間成立，因為結果是隨機化的。

因此，通過比較假設密鑰下的近似表達式與 1/2 的偏差，可以區分出正確或錯誤的密鑰猜測。最後，嘗試所有可能的最後一輪密鑰，看看哪一個的 (P,U) 近似值與 1/2 的偏差最不一致，這個密鑰很可能就是實際的密鑰。

Applying#

Substitution Permutation Network( Hey’s Cipher)#

• 在這個體系中，Heys' Cipher 通過重複的替代和置換操作以及密鑰混合來增強加密的安全性。
• 3 輪 S-box: XORing，所有的 S-box 都是相同的。
• P-box: 置換盒，permuting，它按照特定的規則重新排列位，以擴散每輪中輸入的任何變化。
• 16 位子密鑰: 假設為獨立生成，通常是通過密鑰計劃得到，類似於 DES（數據加密標準）中的做法。
• 例子：每個 probability 都是 input
• 密鑰混合採用的是逐位異或操作。

• E2E 指的是端到端的近似，從明文到密文的整個加密流程。

  

  

  如果你擁有足夠多的明文 - 密文對，理論上你可以利用這種線性近似來解密或更準確地猜測密鑰。

• 如何計算？ 同樣 Matsui’s Lemma

  

  

  關鍵子塊和反推：

  • 目標：生成 Intermediate Ciphertexts，通過 K5 和 C（第二和四個 subset）
  • 和 1st 和 3rd subset 無關，所以 interest 是 2nd 和 4th。

  C 到 U，正確 K 得到正確 U，反之亦然

  

  

  Try All Subkeys#

  • 表中只展示了一部分子建，假設有 64 個 subkeys
  • 假設有 10000 個 ptxt-ctxt 對，使用 64 個 subkeys
  • 對於每個 p-c 對，c 和 subkey 生成 p，計算 bias
  • 偏差最大的子鍵通常是正確的，但並不總是。
  • 可以看到 subkeys 為 24 時 bias 最大，候選